Introduction
Graphs represent pieces of information and relations between them. Pieces of information are called nodes, and relations between them are called edges.
We use directed graphs because we want to be able to represent relations like "father" where the direction is important.
The graph is called "unified" because in earlier versions we had separate graphs for world model and knowledge base
Labeled Nodes
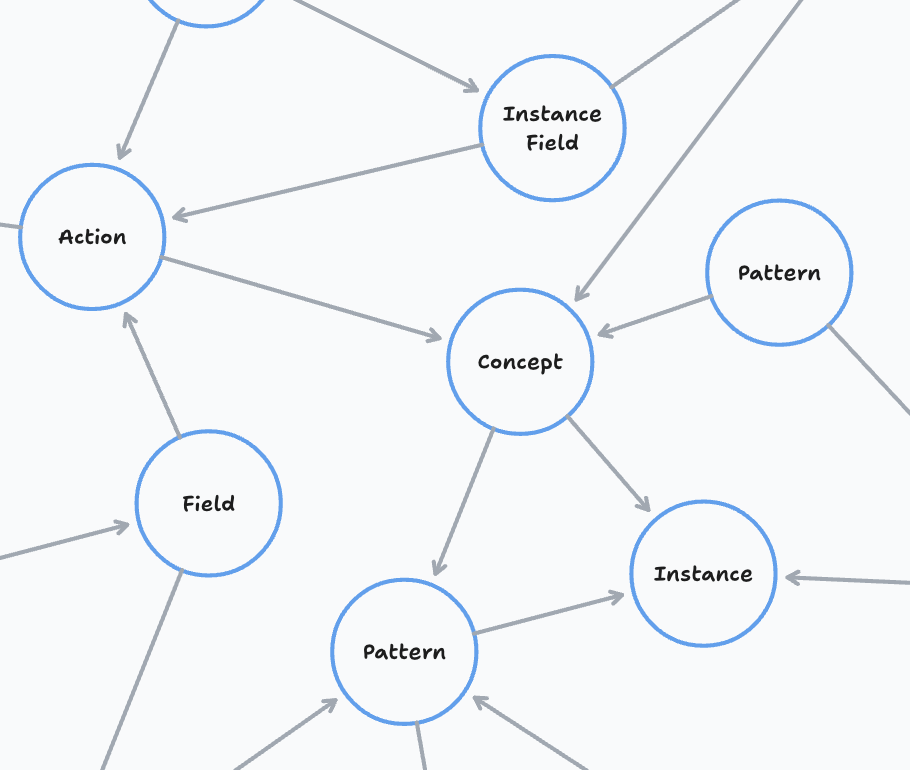
Nodes can have labels that show what kind of information the node represent. For example in the knowledge base we have Concepts and Fields.
All nodes have labels
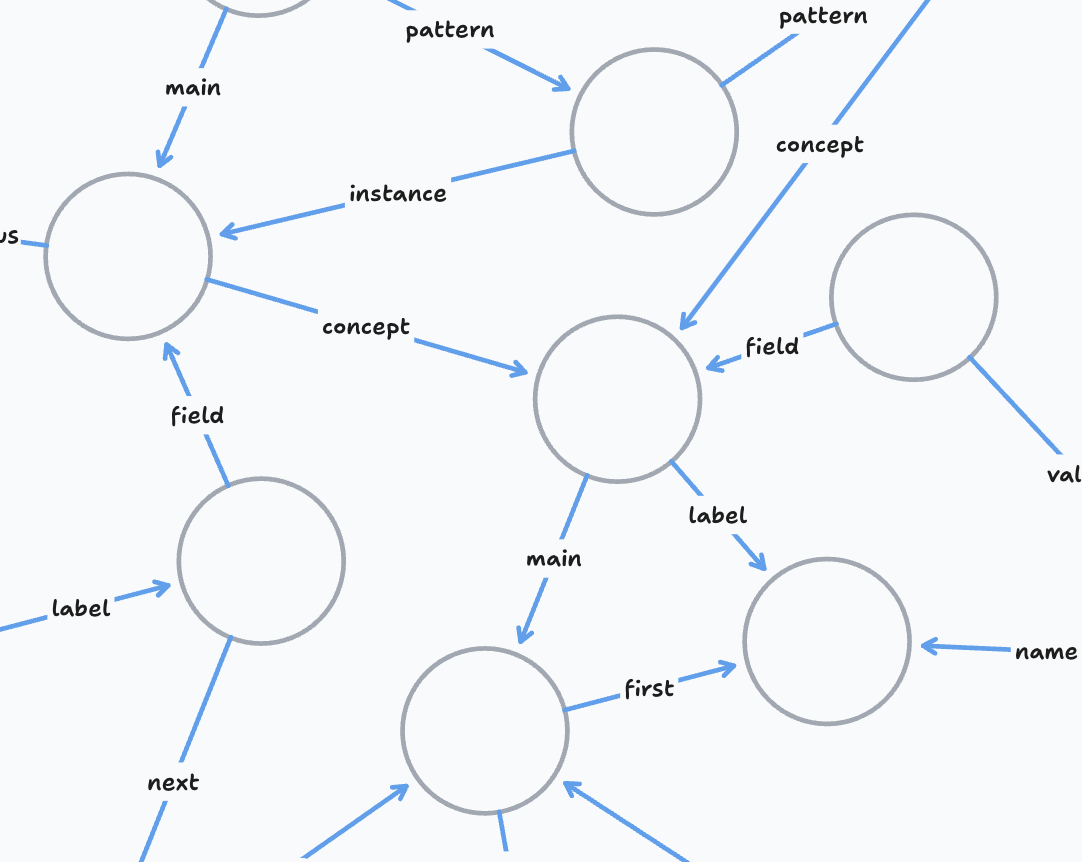
Labeled Edges
Same for edges - there are different types of relations between nodes and we want to be able to distinguish between them.
All edges have labels
Weighted Nodes
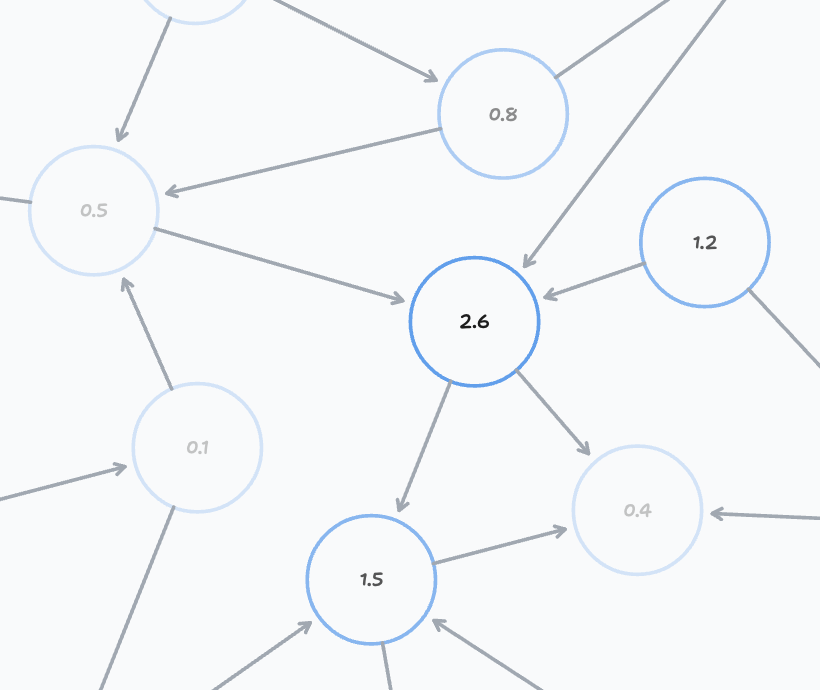
It is often useful to know which nodes are more active than others. For example when in the context of stock market the word "Apple" would likely reffer to the concept of the Apple company, not the fruit. This is achieved by giving more weight to the concept of the company.
On the image we show only weights, but all nodes have both labels and weights.
Weighted Edges
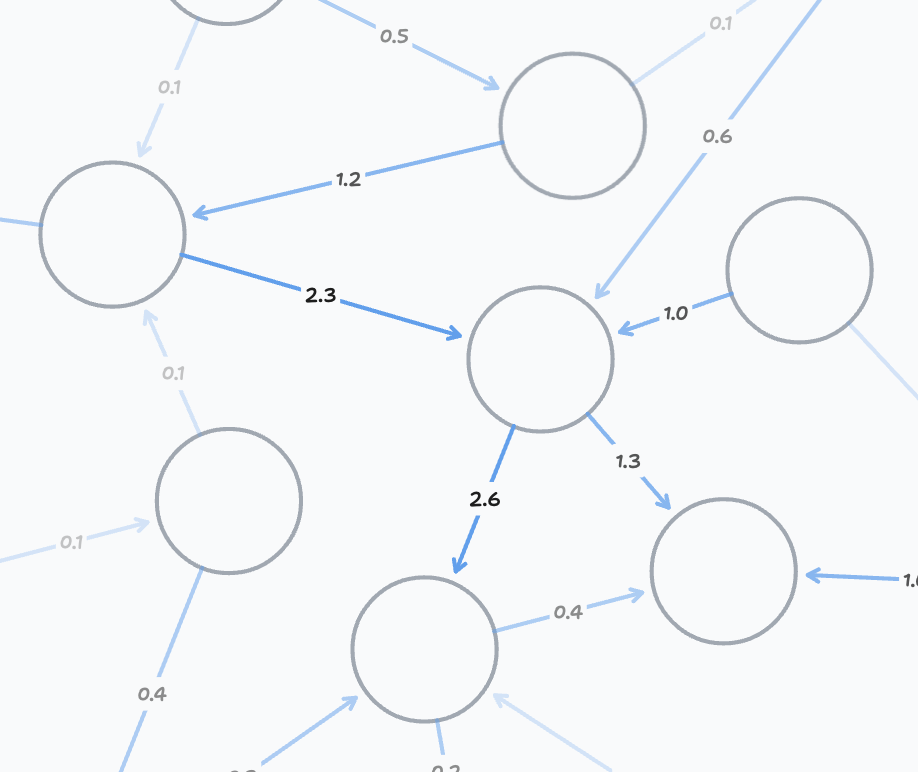
Edges can also be more or less important. For example word "saw" is more connected to the verb "to see" than to the noun "saw" because it is more commonly used as a verb.
This is represented by having more weight on the edge to the verb.
On the image we show only weights, but all edges have both labels and weights.
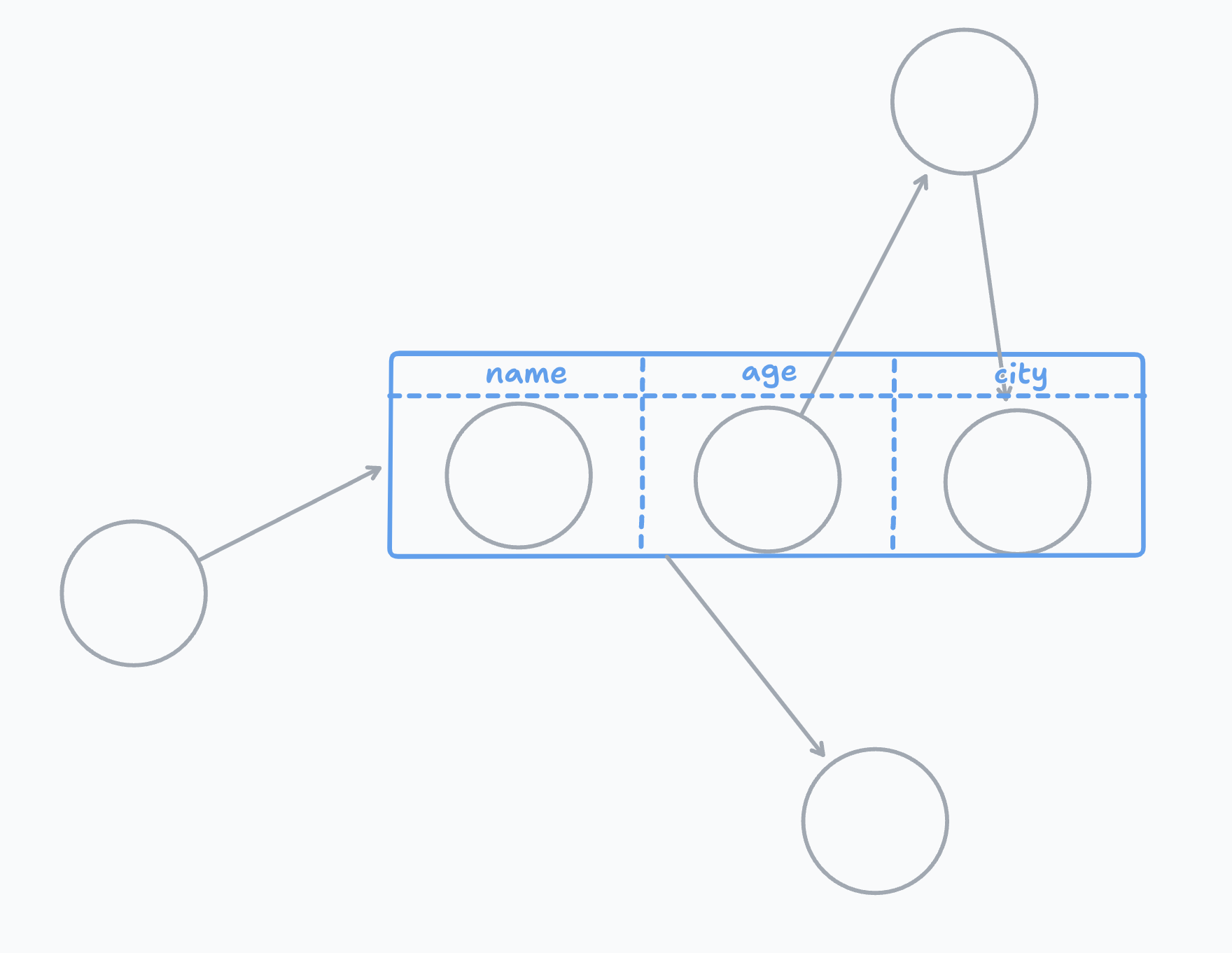
List Nodes
It is often useful to have a one-to-many relation between nodes. If we don't care for the order we can simply have multiple edges going from one node to other nodes.
But if we do care for the order this is a bit more complicated. We could add indices to the edges, but then if we would need to fetch all of them and sort to have them in the correct order.
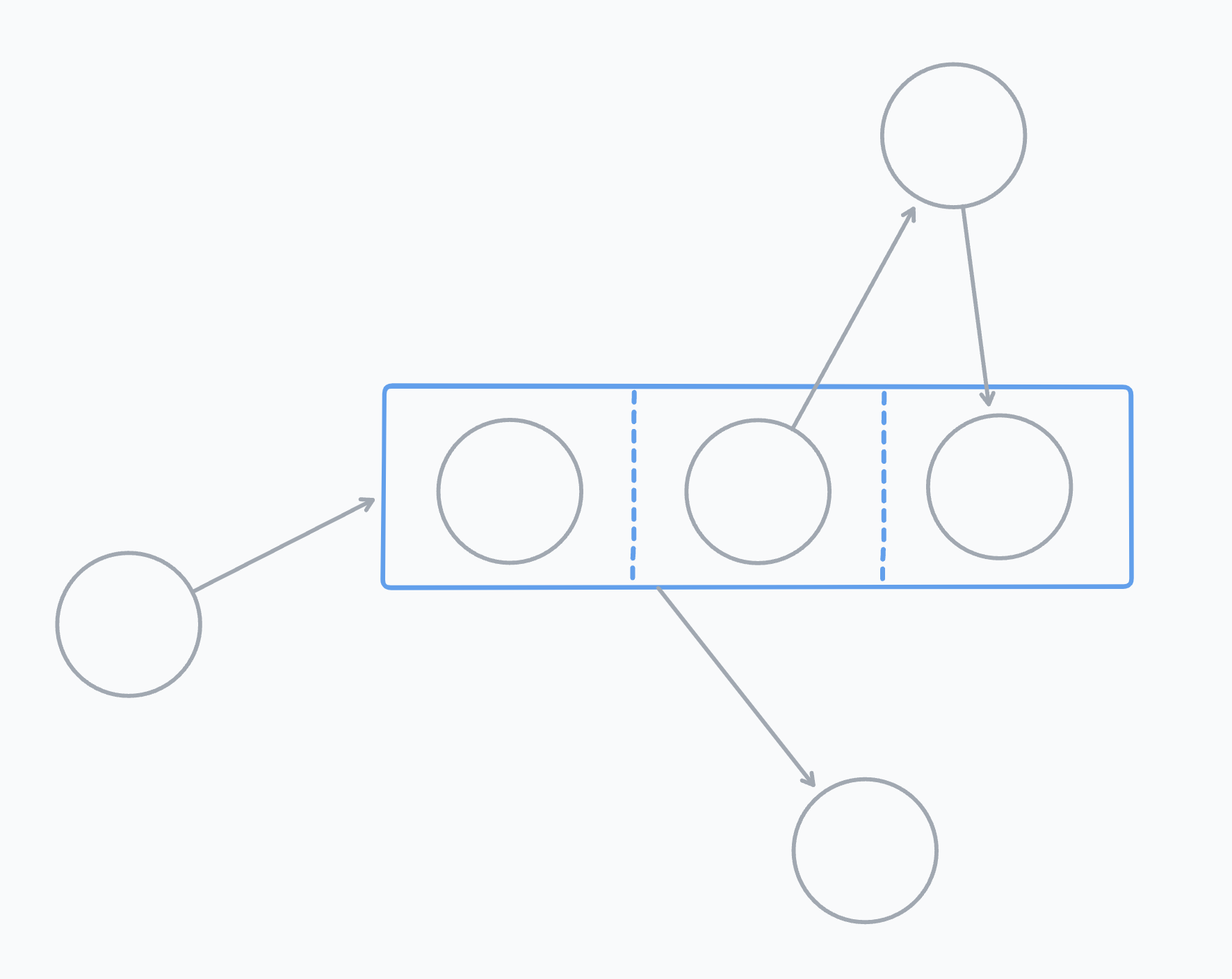
Instead we use List Nodes. It's a node that stores a list of other nodes.
This is our expansion on the idea of hyper-graphs.
Dict Nodes
Same as list node we have dict nodes. They store a key-value mapping from a string to a node.
They also help eliminate unnecessary iteration over the edges.